ASME PTC 19.3 TW-2016 — это отраслевой стандарт, который описывает процедуру оценки термогильз на устойчивость к вихревым колебаниям и статическим нагрузкам в потоке. Методика нужна, чтобы исключить резонанс, чрезмерные напряжения и усталостные повреждения при длительной эксплуатации. Стандарт широко применяется для расчетов термогильз, используемых для контроля температуры технологических процессов в различных отраслях: в энергетике, нефтегазовой и химической промышленности.

В документе изложены подходы к расчету собственной частоты термогильзы с учетом поправок на параметры эксплуатации и геометрию термогильзы, а также методы оценки частоты срыва вихрей, которые определяют динамические нагрузки на термогильзу. Описанные подходы позволяют выполнить расчеты для простых форм термогильз (прямые, конические, ступенчатые) с различными вариантами крепления (сварные, резьбовые, фланцевые).

Для наиболее экстремальных условий эксплуатации рекомендуется использовать геометрии, уменьшающие вероятность возникновения вихревых колебаний, например, термогильзы с спиральными насечками или антивихревыми элементами. Такие дополнительные элементы позволяют отчасти взаимно компенсировать вихревые силы, снижая амплитуду колебаний и сдвигая частоты возбуждения в более безопасные зоны. Такие конструкции термогильз не рассматриваются в ASME PTC 19.3 TW-2016, и для их оценки требуются более сложные методы, включая численное моделирование и экспериментальные исследования. Стандарт также не охватывает вопросы высокочастотных турбулентных возмущений, которые могут быть важны в некоторых случаях.

Ниже — краткий обзор ключевых этапов оценки по стандарту: собственные частоты, вихревая (струхалевская) частота, резонансные зоны и проверка напряжений.

Силы действующие на термогильзу

На рисунке показана система координат и направления сил, которые возникают при обтекании термогильзы потоком:

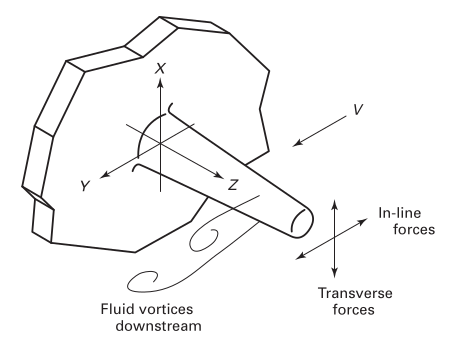
Силы, действующие на термогильзу, помещенную в поток жидкости или газа, можно описать следующим образом:

$$\mathbf{F}(t) = [F_D + F_d \sin(2 \omega_s t)] \mathbf{e}_y + F_L \cos(\omega_s t) \mathbf{e}_x$$

Видно, что на термогильзу действуют три основные силы, две из которых переменные:

Сила	Тип	Направление	Физический смысл
$F_D$	Постоянная	По направлению потока	Установившаяся составляющая силы, связанная с лобовым сопротивлением.
$F_d$	Переменная (продольная)	Вдоль потока	Связана со срывом вихрей при обтекании потоком цилиндрического тела.
$F_L$	Переменная (поперечная)	Перпендикулярно потоку	Также связана со срывом вихрей.

Как видно из формулы, частоты двух переменных сил отличаются вдвое: $F_L$ возбуждается на частоте $f_s=\frac{\omega_s}{2\pi}$, а $F_d$ — на удвоенной частоте $2 f_s$. Величину $f_s$ условимся называть частотой Струхаля. Она зависит от параметров потока и геометрии термогильзы.

В свою очередь величина силы $F_\alpha$ может быть представлена как произведение некоторого эффективного давления, создаваемого потоком, и проекции площади термогильзы на плоскость, перпендикулярную направлению силы.

$$F_\alpha = P_\alpha A_{projected}$$

То есть мы можем выделить два множителя, один из которых зависит только от геометрии термогильзы, а другой — от свойств потока. Нас, однако, будет интересовать не величина силы, а величина изгибающего момента, который в конечном итоге связан с напряжением в материале термогильзы, которое нам и нужно оценить, чтобы сделать вывод о прочности конструкции.

Изгибающий момент (произведение величины силы на плечо) можно оценить по формуле:

$$M_\alpha = P_\alpha \int_{z_0}^L D(z)(z - z_0) dz$$

Здесь $z_0$ — точка в которой нужно оценить момент (обычно это точка закрепления термогильзы). Если часть термогильзы скрыта от потока, то нижний предел интегрирования нужно сдвинуть в точку, где поток начинает оказывать влияние на термогильзу. $D(z)$ — диаметр термогильзы в зависимости от координаты $z$ (для прямой термогильзы это константа $A$).

Изгибающий момент связан с напряжением в материале следующим образом:

$$S_\alpha = \frac{M_\alpha y}{I}$$

Где $y$ — расстояние от нейтральной оси, $I=\pi(D^4-d^4)/64$ — второй момент инерции сечения.

Максимальные напряжения, как правило, возникают в зоне закрепления термогильзы, где момент действующих сил максимальный. Расстояние от нейтральной оси $y$ в точке максимального напряжения равно $A/2$. Подставляя это в формулу для напряжения, получаем:

$$S_\alpha = P_\alpha \frac{32 A}{\pi \left[A^4 -d^4\right]} \int_{z_0}^L D(z)(z - z_0) dz$$

Величина

$$G = \frac{32 A}{\pi \left[A^4 -d^4\right]} \int_{z_0}^L D(z)(z - z_0) dz$$

зависит только от геометрии термогильзы.

Эффективное давление $P_\alpha \propto \frac{\rho V^2}{2}$ зависит только от свойств потока. Для разных типов сил оно оценивается по-разному с использованием соответствующих коэффициентов:

$$P_D = C_D \frac{\rho V^2}{2}, \quad P_d = C_d \frac{\rho V^2}{2}, \quad P_L = C_L \frac{\rho V^2}{2}$$

Стандарт ASME PTC 19.3 TW-2016 рекомендует использовать следующие значения коэффициентов:

Коэффициент	Значение
$C_D$	$1.4$
$C_d$	$0.1$
$C_L$	$1.0$

Собственная частота термогильзы

Явление резонанса возникает, когда частота возбуждающей силы совпадает с собственной частотой конструкции. Поэтому первый шаг оценки по PTC 19.3 TW-2016 — расчет собственной частоты термогильзы. Она зависит от геометрии, материала, условий закрепления и присоединенной массы.

Таким образом, для корректной оценки частоты собственных колебаний термогильзы, вычисленную исходя из геометрии и материала частоту нужно домножить на несколько поправочных коэффициентов, которые позволяют учесть влияние присоединенной массы жидкости, датчика и податливости опоры.

Геометрические параметры термогильзы показаны на рисунке:

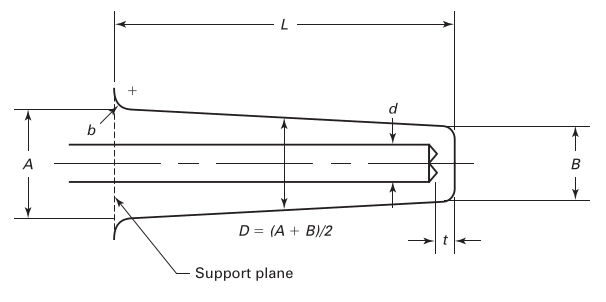
Частота собственных колебаний полого цилиндра, закрепленного жестко у основания может быть приближенно оценена по формуле:

$$f_a = \frac{1.875^2}{2\pi L^2} \sqrt{\frac{E I}{\rho_l}}$$

Где $L$ — длина термогильзы, $E$ — модуль упругости материала при заданной температуре, $I=\pi(D^4-d^4)/64$ — второй момент инерции сечения, $\rho_l=\rho_m\pi(D^2-d^2)/4$ — линейная плотность (масса на единицу длины) термогильзы, выполненной из материала с плотностью $\rho_m$.

Поправочный коэффициент для учета геометрии термогильзы (для случая прямой или конической) задается формулой:

$$H_f = \frac{0.99[1 + (1 - B/A) + (1 - B/A)^2]}{1 + 1.1(D/L)^{3 [1 - 0.8 (d/D)]}}$$

Для тонких прямых термогильз, где $L/A > 10$ этот коэффициент примерно равен $1$, тогда как для конических он может значительно варьироваться в зависимости от геометрии и составлять от $0.6$ до $1.5$.

Поправочный коэффициент для учета присоединенной массы вычисляется по формуле:

$$H_{a,f} = 1 - \frac{\rho}{2 \rho_m}$$

Где $\rho$ — плотность среды (жидкости или газа). Для пара и подобных газов этот коэффициент можно считать равным $1$, тогда как для воды $0.94$ и еще меньше для более плотных жидкостей.

Поправочный коэффициент для учета плотности датчика, вставленного в термогильзу, можно оценить так:

$$H_{a,s} = 1 - \frac{\rho_s}{2 \rho_m}\left[\frac{1}{(D/d)^2 - 1}\right]$$

Где $\rho_s$ — средняя плотность материала датчика. Приблизительно можно считать $\rho_s \approx 2700 кг/м^3$. Эту величину можно использовать в случае, когда нет точных данных о средней плотности датчика.

Поправочный коэффициент для учета податливости опоры термогильзы вычислить сложнее, так как он зависит от типа крепления, от свободной длины термогильзы, от радиуса скругления у основания (параметр $b$ на чертеже) и даже от жесткости стенки трубы. Если точных данных о радиусе скругления $b$ нет, можно принять $b = 0$ в качестве консервативной оценки. Что касается свободной длины термогильзы, то ее также лучше оценивать консервативно. Для фланцевого соединения свободная длина отсчитывается от плоскости фланца, для сварного соединения — от начала сварного шва, для резьбового — от первого витка резьбы.

На рисунках ниже показаны примеры резбового и сварного соединений термогильзы:

Общая формула для оценки поправочного коэффициента податливости опоры термогильзы выглядит так:

$$H_{c} = 1 - \frac{E}{K_M}\frac{\pi (A^4 - d^4)}{32 L [1 + 1.5(b/A)^2]}$$

Где $K_M$ — коэффициент жесткости опоры, который зависит от типа крепления, а $E$ — модуль упругости материала термогильзы. Коэффициент жесткости опоры $K_M$ пропорционален модулю упругости материала и для круглого сечения диаметром $D$ может быть оценен по формуле:

$$K_M = \frac{E}{0.787}\left(\frac{D}{2}\right)^3$$

На практике, принимая во внимание, что в общей формуле фигурируют 4-ые степени внешнего диаметра и полости, которая обычно значительно меньше внешнего диаметра, можно упростить расчет и считать:

$$H_c = 1 - 0.61\frac{A}{L[1 + 1.5(b/A)]^2}$$

В случае резьбового соединения нужно принимать во внимание, что такой тип крепления обычно менее жесткий, чем сварной или фланцевый. Поэтому для резьбового соединения рекомендуется использовать следующую формулу, где используется меньший коэффициент жесткости, а радиус скругления принимается равным нулю:

$$H_c = 1 - 0.9\frac{A}{L}$$

Таким образом, окончательная формула для оценки собственной частоты термогильзы по ASME PTC 19.3 TW-2016 принимает вид:

$$f^c_n = H_c H_f H_{a,f} H_{a,s} f_a$$

Частота Струхаля (вихревая частота)

Теперь нам необходимо оценить частоту срыва вихрей, которая определяет частоты возбуждающих сил. Эта частота зависит от свойств обтекающей среды (скорости потока, вязкости, плотности) и геометрии термогильзы.

Число Струхаля $N_s$ - это безразмерный параметр, один из критериев подобия нестационарных течений жидкостей и газов. Для колебательных процессов число Струхаля связано с частотой этих процессов следующим образом:

$$ f_s = \frac{N_s V}{B} $$

Где $f_s$ — частота срыва вихрей, $B$ — характерный размер тела (в данном случае диаметр наконечника термогильзы), $V$ — характерная скорость потока.

Для случая поперечного обтекания цилиндра число Струхаля зависит в основном от числа Рейнольдса $Re$ и для широкого диапазона величин числа Рейнольдса, на практике соответствующего условиям эксплуатации термогильз, существует эмпирический закон постоянства числа Струхаля $N_s \approx 0.2$, что упрощает расчеты.

В стандарте ASME PTC 19.3 TW-2016 рекомендуется использовать консервативное значение $N_s = 0.22$.

Резонанс

Напомним, что вихревые явления приводят к двум типам периодических сил, действующих в двух разных направлениях: поперечная (traverse) на частоте $f_s$ и продольная (in-line) на частоте $2 f_s$. Очевидно, что при приближении этих частот к собственной частоте термогильзы возникает риск резонанса.

Частота Струхаля линейно растет с увеличением скорости потока, и можно расчитать при каких скоростях потока возникает резонанс.

Для продольной периодической силы (in-line), соответствующей удвоенной струхалевской частоте, критическая скорость потока рассчитывается по формуле:

$$ V_{IR} = \frac{f^c_n B}{2 N_s} $$

Соответственно, резонанс в поперечном направлении (traverse) возникает примерно при двухкратной скорости продольного резонанса.

Резонанс может многократно усиливать воздействие периодических сил на термогильзу, что приводит к значительному увеличению напряжений в материале. Для корректной оценки напряжений при резонансе необходимо учитывать также и демпфирующие свойства системы.

Документ ASME PTC 19.3 TW-2016 рекомендует использовать усиливающие коэффициенты, которые зависят от соотношения собственной частоты термогильзы и частоты возбуждающих сил. Соответственно чем ближе эти частоты, тем больше коэффициент усиления.

Для продольных колебаний:

$$\Phi_d = \frac{1}{1 - \left(2 f_s/f^c_n\right)^2}$$

Для поперечных колебаний:

$$\Phi_L = \frac{1}{1 - \left(f_s/f^c_n\right)^2}$$

Как видно из формул, при совпадении коэффициенты стремятся к бесконечности, что не имеет физического смысла. На практике эти формулы применимы вне диапазонов $0.8 \lt \frac{f_s}{f^c_n} \lt 1.2$ и $0.8 \lt \frac{2 f_s}{f^c_n} \lt 1.2$, а масксимальные значения коэффициентов усиления при резонансе ограничены величиной $\frac{1}{2\zeta}$, где $\zeta$ — коэффициент демпфирования системы. Если демпфирующий коэффициент неизвестен, стандарт рекомендует использовать значение $\zeta = 0.0005$.

Динамическое напряжение

Как мы привели выше в разделе о силах, действующих на термогильзу, напряжение в материале термогильзы у основания, при воздействии на нее периодических сил, можно оценить по формулам:

Для продольных (in-line) периодических сил с учетом усиливающего коэффициента:

$$S_d = \Phi_d G C_d \frac{\rho V^2}{2}$$

Для поперечных (traverse) периодических сил с учетом усиливающего коэффициента:

$$S_L = \Phi_L G C_L \frac{\rho V^2}{2}$$

Общее колебательное напряжение в материале термогильзы при воздействии обеих сил можно оценить по формуле:

$$S_O = K_t \sqrt{S_d^2 + S_L^2}$$

Где $K_t$ — коэффициент концентрации напряжений, который зависит от геометрии термогильзы и способа закрепления. Рекомендации по его оценке также приведены в стандарте ASME PTC 19.3 TW-2016.

На рисунке приден схематический график зависимости колебательного напряжения от скорости потока (для конкретной термогильзы с заданными параметрами):

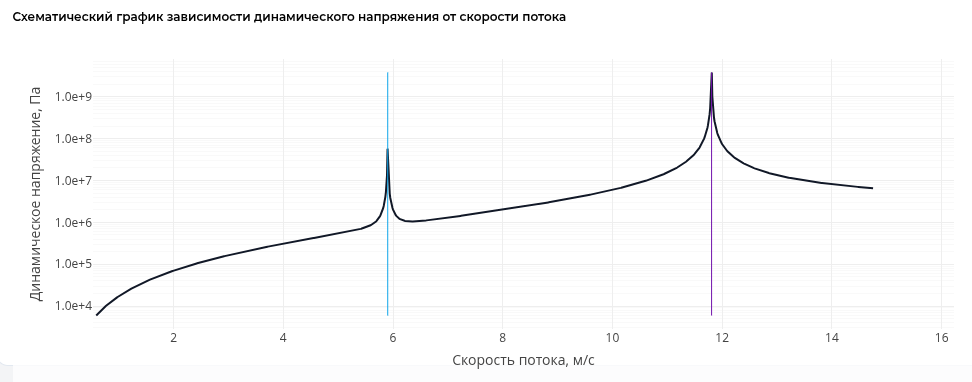
На данном графике кривая расчитана без учета конечности коэффициентов усиления $\Phi_\alpha$ при приближении к резонансным зонам. Видно, что напряжение резко возрастает при приближении к критическим скоростям, отличающимися численно примерно вдвое.

Задача инженера — подобрать для заданных условий эксплуатации такую термогильзу, чтобы частота ее собственных колебаний находилась вне резонансных зон. Наиболее безопасно выбирать термогильзу так, чтобы ее собственная частота была больше даже удвоенной частоты Струхаля, чтобы избежать даже продольного резонанса (первой резонансной зоны). Допустимо в некоторых случаях выбирать термогильзу с такой собственной частотой, чтобы рабочая точка находилась между первой и второй резонансными зонами, но это требует более тщательной оценки условий эксплуатации. В любом случае, напряжения не должны превышать предела усталостной прочности материала термогильзы с учтом поправочных коэффициентов на температуру и коррозию.

Стационарное (steady) напряжение

При эксплуатации термогильзы в потоке с низкой скоростью, поток не передает значительных импульсов термогильзе, и напряжения в материале определяются в основном стационарными силами, связанными с давлением жидкости или газа.

При возрастании скорости потока жидкость начинает оказывать воздействие на термогильзу. До тех пор пока вихревое воздействие мало преобладает лобовое сопротивление потоку. Никаких значительных колебательных воздействий может не возникать, но тем не менее напряжения в материале термогильзы будут расти с увеличением скорости потока.

Для оценки устойчивости термогильзы к напряжениям, связанным со стационарными силами, стандарт ASME PTC 19.3 TW-2016 рекомендует использовать критерий Мизеса:

$$\sqrt{\frac{(S_{max} - S_r)^2 + (S_{max} - S_t)^2 + (S_t - S_r)^2}{2}} \le 1.5 S$$

Здесь $S$ предельная допустимое напряжение для материала.

Максимальное напряжение в материале термогильзы, вызванное стационарными силами:

$$S_{max} = S_D + S_a$$

Аксиальное напряжение в материале термогильзы, вызванное давлением среды:

$$S_a = \frac{P}{1 - (d/A)^2}$$

Радиальное напряжение в материале термогильзы, вызванное давлением среды:

$$S_r = P$$

Тангенциальное напряжение в материале термогильзы, вызванное давлением среды:

$$S_t = P \frac{(1 + (d/A)^2)}{1 - (d/A)^2}$$

Критерии оценки термогильзы по ASME PTC 19.3 TW-2016

PTC 19.3 TW-2016 требует, чтобы термогильза проходила следующие проверки:

• достаточный запас по частотному соотношению для поперечной и продольной частоты, чтобы избежать резонансных зон
• динамические напряжения ниже допустимых значений, а также запас по усталостной прочности
• стационарные (steady) напряжения в пределах допустимых значений

Если по каким-то критериям термогильза не проходит расчет, стандарт допускает изменение геометрии, материала, варианта крепления или условий эксплуатации (например, снижение скорости потока).